顶点坐标 万图壁纸网
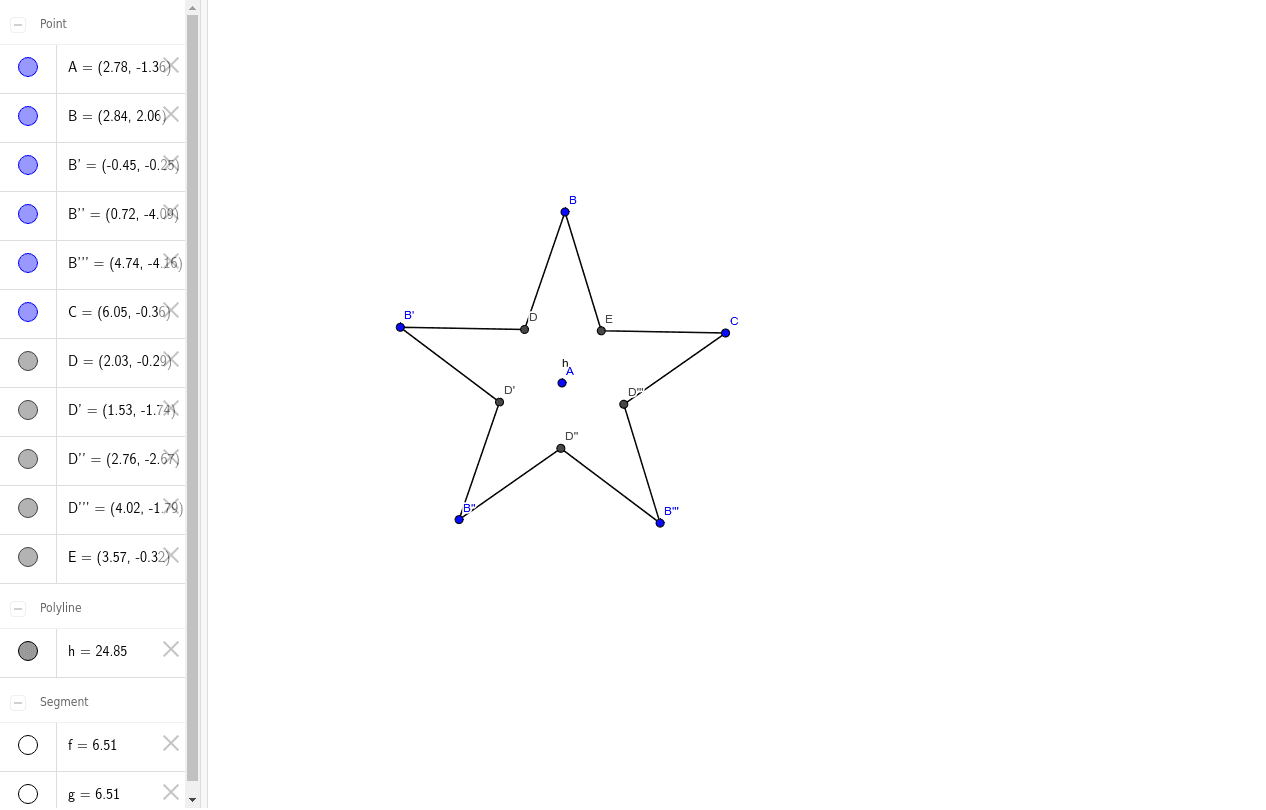
請問這兩題數學ಠ_ಠ "還 "和為正十邊形的連續四個頂點 ,設此十邊形的外接轅直徑 為6,則4讓 及 , ,求四邊形 42 4 如圖正五邊形 4 42 45 4/4y,各邊向外延長形成一五角星,求四邊形 42 4 85 膺與五角星面積比值E 為 謝 4 45 及 45 同 4 史 應三角形の面積を求める 三角形の面積は½ x 底辺 x 高さ(A = ½bh)という計算式で求められます。既に高さが分かっているので、公式に当てはめて、小さな三角形1つの面積を求めましょう。 小さな三角形の面積= ½bh = ½(35)(48) = 84 となります。
五角星 面積 公式
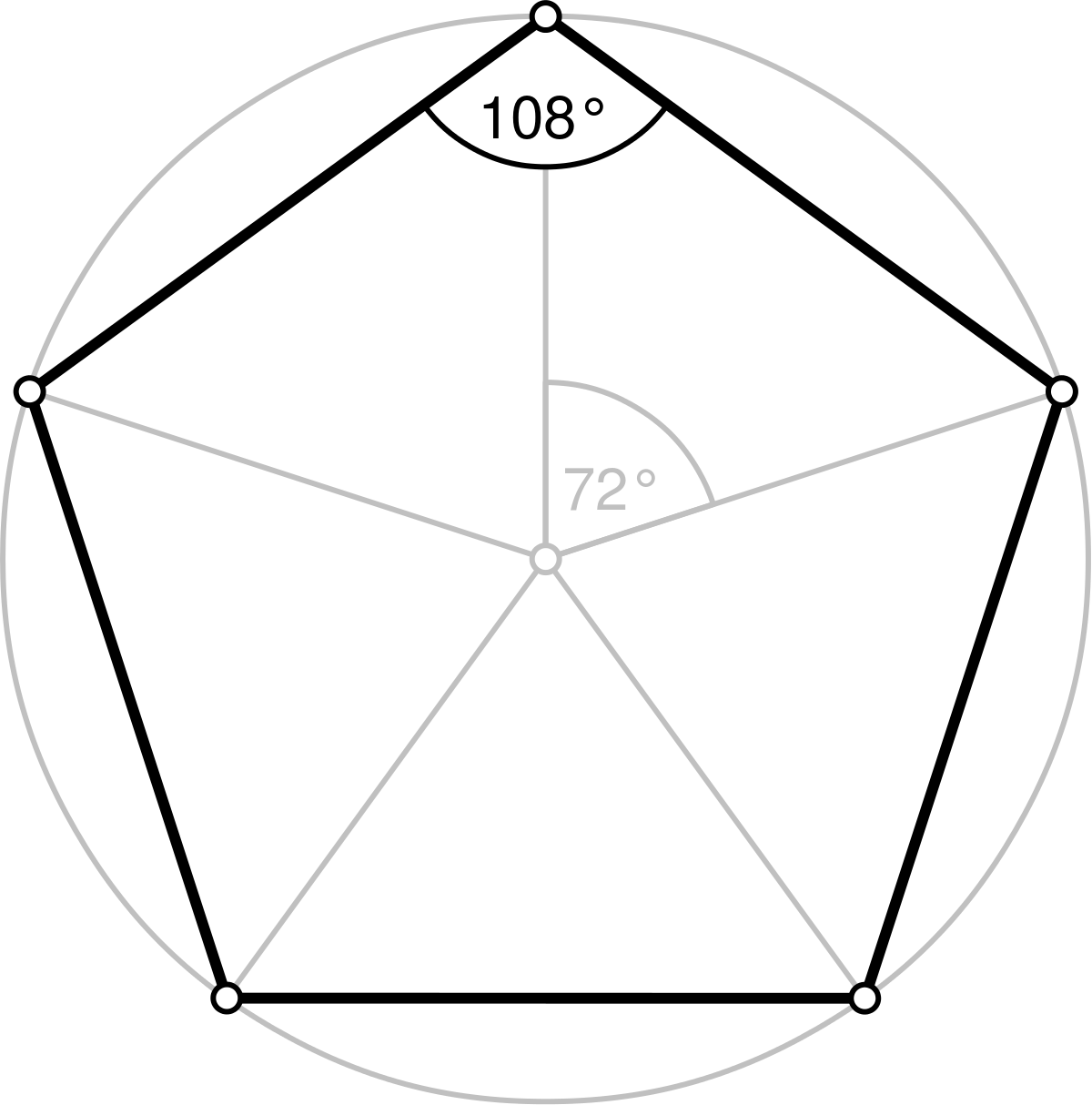
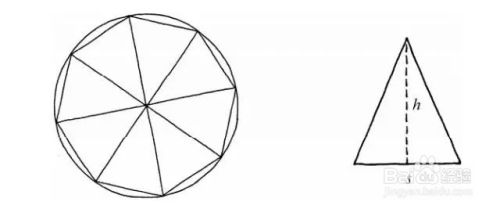
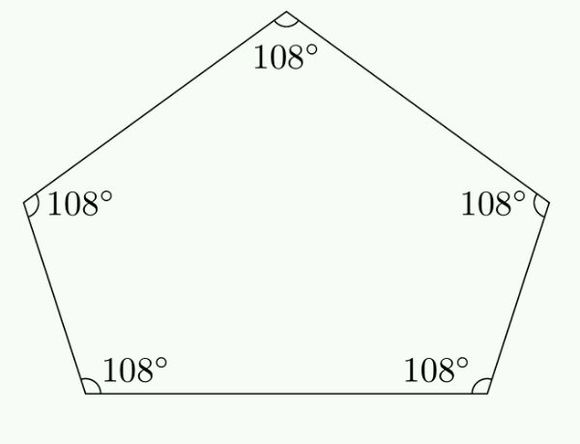
五角星 面積 公式-正五角星的角尖是36度,拐度是108度。 分析: 可以把五角星分成五个相同的等腰直接三角和一个正五边形,如图片。 多边形内角和计算公式:(n - 2)×180°(n大于等于3且n为整数)。問題一:正多邊形的面積公式 5分 設正n邊形的面積為S, 則,S=(1/2)nR^2*sinα=nr^2tan(α/2) 式中,n邊數,R三角形的外接圓的半徑,r三角形的內切圓的半徑,α一邊所對的圓心角( 問題一:五角星的對稱軸怎麼畫,(要圖解) 問題二:怎樣畫軸對稱圖形

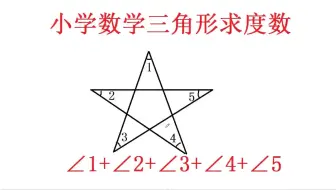
Amc 8 第二讲 任意五角星内角和都是180 怎么证明 知乎
三角形triangle、圆形circle、长方形rectangle、正方形square。 一、三角形Triangle 例句:它的轮廓大致形成一个等边三角形。 Its outline roughly forms an equilateral triangle 二、圆形circle 例句:连衣裙的裙身呈圆形完全展开。 The dress's full skirt fanned out in a bright circl 三所求 585推甄試題 設點在的邊上,且的面積=的面積,若的座標 為 (0,5),的座標為 (7,0),則的座標為 。 答 解析等高三角形面積比其恰等於底邊之比 6 85推甄試題 設想地球是個圓球體,已知沿著赤道,經緯度10度間的距離是1113公里, 那麼平面凸五邊形的最大面積與圓內接 (2n1) 邊形的正弦公式 李輝濱 I 前言 對平面上的任意凸多邊形作適當的圖形分割, 可以求出此凸多邊形面積的一般公式。 分割 一個給定的凸多邊形時, 不同的分割方法, 所求得的面積公式也不盡相同;
乾貨! CAD製圖詳細總結 由 建築工程資料共享 發表于 運動 標註 檢視 物件 圖塊 圖形 簡介 注:最大值右鍵功能取消:工具選項使用者系統配置繪圖區域中不顯示快捷選單密碼設:工具選項開啟和儲存下面的安全選項物件捕捉設定:工具草圖設定物件歡迎前來淘寶網實力旺鋪,選購正版 鈑金展開計算210例鈑金下料常用技術第2版鈑金展開計算法 3冊 鈑金展開技巧書 鉚工鈑金工管工鉗工設計鈑金下料技術圖書籍,該商品由中圖天下圖書專營店鋪提供,有問題可以直接諮詢商家五邊形邊長 為: = , 得到了正確的結果 因此此種構造正五邊形的方法是有效的。 約西元前300年,欧几里得在他的《几何原本》中描述了一个用直尺和圆规做出正五边形的过程。 物理方法
五角星 面積 公式のギャラリー
各画像をクリックすると、ダウンロードまたは拡大表示できます
 |  |  |
 |  |  |
 |  | |
「五角星 面積 公式」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  |  |
 |  | |
 |  |  |
「五角星 面積 公式」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  |  |
 |  | |
 |  | |
「五角星 面積 公式」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  | |
 |  | |
 |  | |
「五角星 面積 公式」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  |  |
 | ||
 | ||
「五角星 面積 公式」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  | |
 | ||
 |  | |
「五角星 面積 公式」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  |  |
 |  | |
 |  | |
「五角星 面積 公式」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  |  |
 |  | |
 |  | |
「五角星 面積 公式」の画像ギャラリー、詳細は各画像をクリックしてください。
 | ||
 |  | |
「五角星 面積 公式」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  | |
 |  |  |
 |  |  |
「五角星 面積 公式」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  |  |
 |  | |
 |  | |
「五角星 面積 公式」の画像ギャラリー、詳細は各画像をクリックしてください。
 | ||
 |
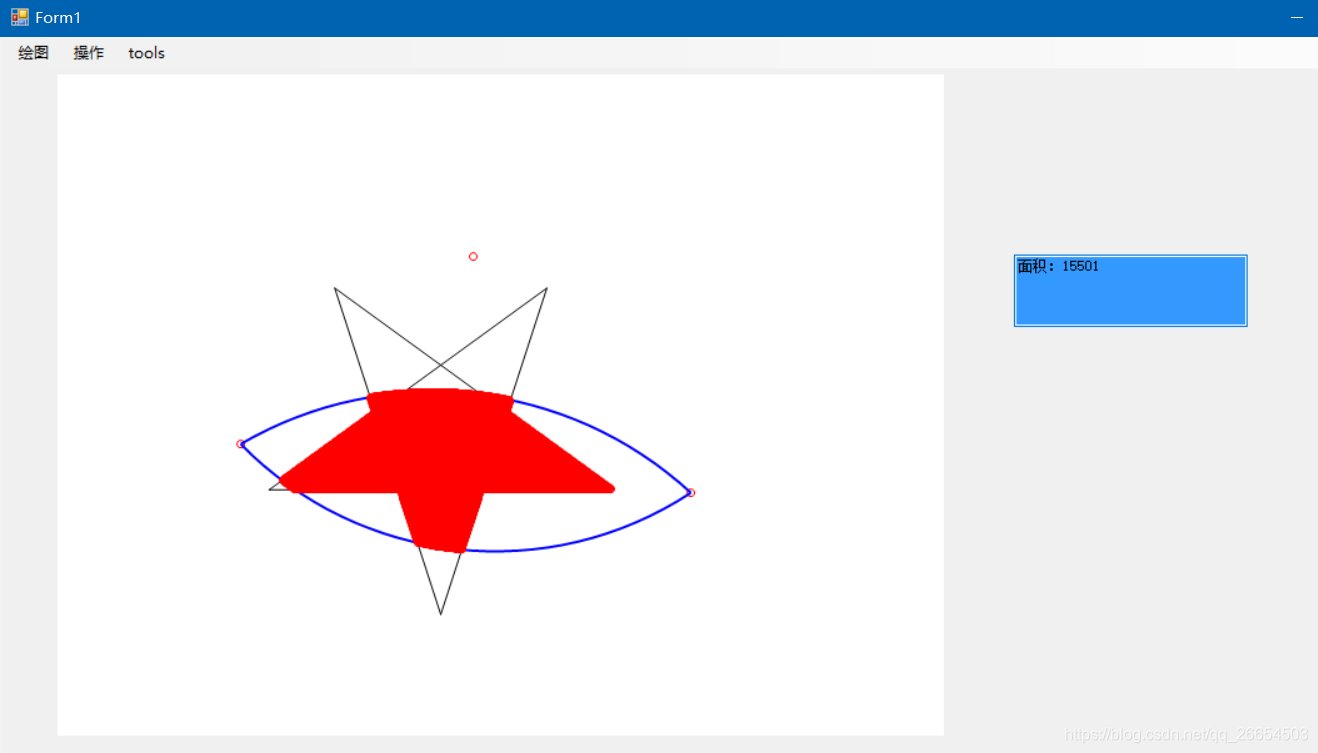
一、查询面积(AREA)命令 1/4 分步阅读 CAD提供了查询面积的命令:AREA,快捷键是AA。 可以在菜单、工具栏和命令面板中调用此命令,但最简单的方法还是输入AA后回车。 我们先来看查询面积有哪些选项,执行查询面积命令后,命令行提示如下: 指定第一个求出了一般形的面積公式後, 接著總要問起:圖形在何種情況下會有最大的面積?而此最大面積的公式形式又如何?會簡潔到何種程度? 在探討凸五邊形的最大面積問題時, 發現到圓內接奇數邊形的多邊形有一特殊性質, 此性質是其各頂角與相對應的各邊長相關聯





0 件のコメント:
コメントを投稿